유체역학에서 Reynolds 수는 관성에 의한 힘과 점성에 의한 힘의 비로서,
주어진 유동 조건에서 이 두 종류의 힘의 상대적인 역학관계를 정량적으로 나타 냅니다.
1880년대 Osborne Reynolds는 많은 실험을 통해 발견하였습니다.
기하학적 형상, 표면조도, 유동속도, 표면온도, 유체의 종류 등이 가장 큰 영향을 미칩니다.
Reynolds 수는 유체 동역학에서 가장 중요한 무차원 수 중 하나이며,
다른 무창원 수들과 함께 사용되어 동적 상사성을 판별하는 기준이 됩니다.
두 유동 패턴이 기하학적으로 상사일 때, 이 두 유동의 주요 무차원 수들이 동일한 값을 가지면,
이 두 유동이 동적 상사성을 가졌다고 말하며 이 두 유동은 그 형태가 유사하게 됩니다.
또한, 유동이 층류인지 난류인지를 예측하는 데에도 Reynolds 수는 사용됩니다.
층류는 점성력이 지배적인 유동으로서 레이놀즈 수가 낮고, 평탄하면서도 일정한 유동이 특징이며,
난류는 관성력이 지배적인 유동으로서 레이놀즈 수가 높고, 임의적인 와류, 기타 유동의 변동이 특징입니다.
Reynolds 수 정의는 다음 식과 같습니다.
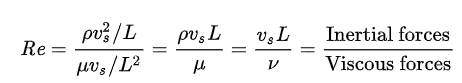
여기서 Vs는 유동의 평균속도, L은 특성 길이(characteristic length), μ는 유체의 점성 계수(Dynamic Viscosity)
ν는 유체의 동점성 계수(Kinematic Viscosity), ρ는 유체의 밀도입니다.
특성 길이란 예를 들면 단면이 원형인 파이프 내의 유동에 대해서는 파이프의 지름이 되며, 단면이 원형이
아닌 경우 특성 길이는 수력학적 직경으로 정의된다. 평판 위를 흐르는 유동의 경우, 특성 길이는 평판의 길이이다.
층류, 천이, 난류유동에 대한 정확한 Reynolds 수를 알면 좋겠으나 실제는 그렇지 못합니다.
층류에서 난류로의 천이는 표면조도, 파이프 진동 그리고 유동내부의 요동 등에 영향을 받기 때문입니다.
대체로 원형 파이프 유동의 경우 다음과 같이 Re≤2300이면 층류, Re≥4000이면 난류 그리고 그 사이가 천이영역으로 구
분됩니다.
Re≤2300 층류 laminar flow
2300≤Re≤4000 천이영역 transitional flow
4000≤Re 난류 turbulent flow
천이 유동에서는 층류와 난류가 임의적으로 반복됩니다. 파이프 내부 표면이 아주 매끈하고 파이프 진동과 유동의
교란이 없는 경우에는 매우 높은 Reynolds 수에서도 층류가 될 수 있음을 기억하여야 합니다.
여기까지 유동의 특성을 구분지는 Reynolds 수를 공부하였습니다.
'전공' 카테고리의 다른 글
| [유체역학] 층류와 난류 (0) | 2022.02.05 |
|---|---|
| [유체역학] 파이프 내의 유동 (0) | 2022.01.17 |
| [유체역학] 항력과 양력 (0) | 2022.01.15 |
| [유체역학] Bernoulli 방정식 (0) | 2022.01.14 |
| [유체역학] 유체의 상태량? (0) | 2022.01.02 |