오늘은 전산유체역학에서 잠시 나왔던 나비에 스토크스 방정식(Navier-Stokes equation)에 대해서 자세히 알아보도록 하겠습니다. 나비에 스토크스 방정식(Navier-Stokes equation)은 일정한 상태량을 갖는 비압축성 뉴턴 유체에 대한 선형 운동량 보존에 관한 방정식입니다.
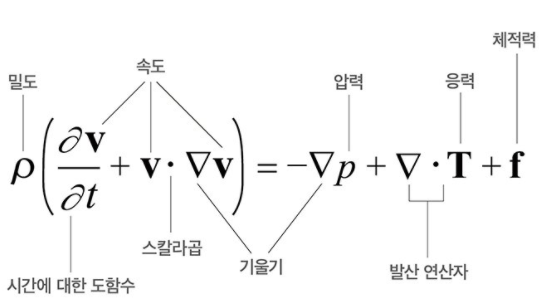
나비에 스토그스 방정식(Navier-Stokes, eaquation) (출처: 세계를 바꾼 17가지 방정식(사이언스북스, 2016)
프랑스 물리학자 클로드-루이 나비에와 영국 수학자 조지 스토크스가 뉴턴의 운동 제2법칙(F=ma)를 유체역학에서 사용하기 쉽게 운동량을 기준으로 세운 수지식입니다. 이 방정식은 물리학의 수많은 곳에서 널리 사용되고 있습니다. 하지만 문헌상에서 이용 가능한 해석 해는 거의 존재하지 않으며, 그러한 해는 손꼽을 정도로 매우 적습니다. 실제 거의 대부분의 유체역학 문제는 해석적으로 풀 수 없으며, 근사적 방법이나 컴퓨터의 도움이 필요로 합니다.
앞선 말한 것 처럼 나비에 스토크스 방정식(Navier-Stokes equation)은 뉴턴의 제2법칙인 F=ma를 유체역학에서 사용하기 편하게 그 형태를 바꾼 것 입니다. 유체는 고체와 달리 고정된 좌표 개념이 없기 때문에 분석이 매우 힘듭니다. 따라서 유체에 뉴턴 역학을 적용하기 위해서는 다른 방식이 필요하고, 이 방식에 따라 운동량 보존 법칙을 재정리한 것이 이 방정식입니다. 유체역학에서 중요한 물리량은 질량, 운동량, 에너지이며 이 세가지 물리량의 보존 법칙이 유체역학에서의 지배방정식이 되고, 그 중 가장 중요한 방정식이 나비에 스토크스 방정식(Navier-Stokes equation)입니다.
이 수식을 통해 유체에 대한 운동을 확인 할 수 있습니다. 항공기가 뜨는 원리, 담배연기 확산, 기계의 내부유로 설계, 날씨예보 등에 쓰입니다. 세계를 바꾼 가장 주요한 수식 중에 하나가 아닐 수가 없습니다.


나비에 스토크스 방정식(Navier-Stokes equation) 유체의 압축성을 나타냅니다. 오일러 방정식(Euler equation)에 점성항을 더한 것이 나비에 스토크스 방정식(Navier-Stokes equation)입니다.

오일러 방정식(Euler equation)은 비점성 영역을 나타낸 방정식이며, 나비에 스토크스 방정식(Navier-Stokes equation)의 근사화라고 볼 수 있습니다.
간단하게 나비에 스토크스 방정식(Navier-Stokes equation)에 대해서 확인하여 보았습니다. 아직도 나비에 스토크스 방정식(Navier-Stokes equation)은 해의 존재성 조차 모르는 수식입니다. 난해한 수식이라고 볼 수 있습니다. 하지만 우리 삶에서 많은 도움을 주고 있는 수식이기도 합니다. 현재 미국 클레이 연구소에서는 밀레니엄 난제로 등록되어 있기도 합니다. 수치해석으로 얻은 근사 값으로도 우리 삶을 이끌고 있는 나비에 스토크스 방정식(Navier-Stokes equation) 답이 나오는 그 날이 왔으면 좋겠습니다.
'전공' 카테고리의 다른 글
| [유체역학] 항력과 양력 (0) | 2022.01.15 |
|---|---|
| [유체역학] Bernoulli 방정식 (0) | 2022.01.14 |
| [유체역학] 유체의 상태량? (0) | 2022.01.02 |
| [유체역학] 유체역학 이란? (0) | 2021.12.31 |
| [유체역학] 전산 유체 역학 이란? (0) | 2021.12.21 |